The Regression Effect Is Best Described as

The mediational effect in which X leads to Y through M is called the indirect effect. Depending on the software used this information may be provided.

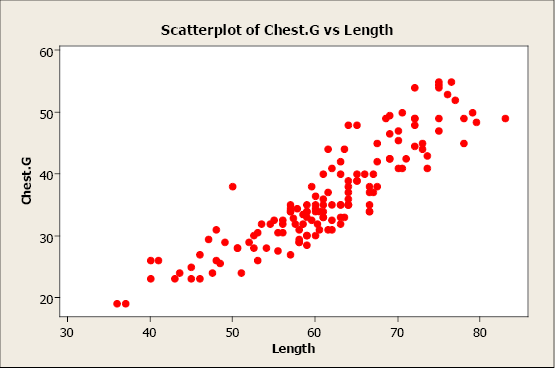
Chapter 7 Correlation And Simple Linear Regression Natural Resources Biometrics

E is the energy usage over the period in question a month in the example above.

. We could use the Excel Regression tool although here we use the Real Statistics Linear Regression data analysis tool as described in Multiple Regression Analysis on the X input in range E5F16 and Y input in range G5G16. When the constant y intercept differs between regression equations the regression lines are shifted up or down on the y-axis. A fitted linear regression model can be used to identify the relationship between a single predictor variable x j and the response variable y when all the other predictor variables in the model are held fixed.

In marketing this is known as a synergy effect and in statistics it is referred to as an interaction effect James et al. HDD is the heating degree days over the period in question a month in the example above. It also depends on the values of B3 and Sun.

The indirect effect represents the portion of the relationship between X and Y that is mediated by M. Other regression models can equally be used such as ordinary least squares linear regression for continuous outcomes for example the duration of cycling trips in an ITS study looking at the impact of public transport strikes on usage of a bicycle share programme in London21 Most of the steps described in this tutorial remain the same for the analysis of. We next run regression data analysis on the log-transformed data.

In regression analysis all the measured baseline confounders are included as predictors to the outcome. In statistical modeling regression analysis is a set of statistical processes for estimating the relationships between a dependent variable often called the outcome or response variable and one or more independent variables often called predictors covariates explanatory variables or features. These two models have different constants.

Regression analysis is another popular adjustment method. Testing for mediation Baron and Kenny 1986 proposed a four step approach in. Specifically the interpretation of β j is the expected change in y for a one-unit change in x j when the other covariates are held fixedthat is the expected value of the.

The proportional hazards assumption can be tested by examining the residuals of the model. B1 is now interpreted as the unique effect of Bacteria on Height only when Sun 0. The output is shown in Figure 2.

We now discuss the meaning of each of the quantities in 21. It is also called the two-variable linear regression model or bivariate linear regression modelbecause it relates the two variables x and y. The equation of multiple linear regression with interaction.

Well use a hypothesis test to determine whether this vertical shift is. Log odds could be converted to normal odds using the exponential function eg a logistic regression intercept of 2 corresponds to odds of e2739 meaning that the target outcome eg a correct response was about 7 times more likely than the non-target. The scatterplot below shows how the output for Condition B is consistently higher than Condition A for any given Input.

In situations when the proportional hazards assumption of the Cox regression model does not hold we say that the effect of the covariate is time-varying. A is the slope of the regression line. In this chapter youll learn.

Log odds are difficult to interpret on their own but they can be translated using the formulae described above. They also have a random component that causes them to be scattered somewhat around that best fit line. The rejection of the null hypothesis induces the use of time varying coefficient to describe the data.

This adjustment can produce the average causal effect and average causal effect on the treated. A and c are the regression coefficients different for every regression. Incidentally the term regression has origins that are not especially important for most modern econometric.

Regression analysis is a widely used technique which is useful for evaluating multiple independent variables. The most common form of regression analysis is linear regression in which one. The unique effect of Bacteria is represented by everything that is multiplied by Bacteria in the model.

Procedures to test whether an observed sample correlation is suggestive of a statistically significant correlation are described in detail in Kleinbaum Kupper and Muller. These data have a linear component that can be described by a best fit line having a non-zero slope. There are three major disadvantages for this method Schafer and Kang 2008.

A regression analysis of these data calculates that the equation of the best fit line is y 6x 55. As a result it is particularly useful. Regression equation for heating no cooling with no day normalization E aHDD c Where.

R codes for computing the regression coefficients associated with the main effects and the interaction effects. So the unique effect of Bacteria on Height is not limited to B1.

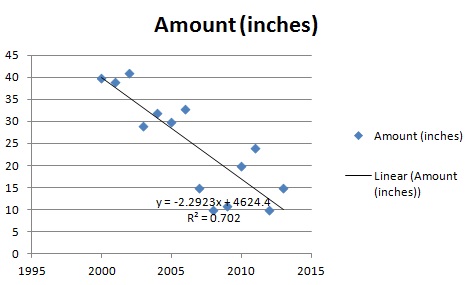
Regression Analysis Step By Step Articles Videos Simple Definitions

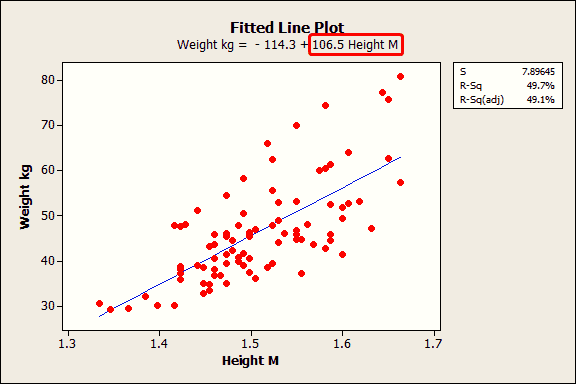
How To Interpret P Values And Coefficients In Regression Analysis Statistics By Jim

Linear Relationship Definition

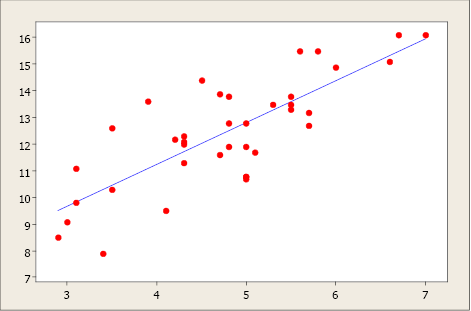
Chapter 7 Correlation And Simple Linear Regression Natural Resources Biometrics